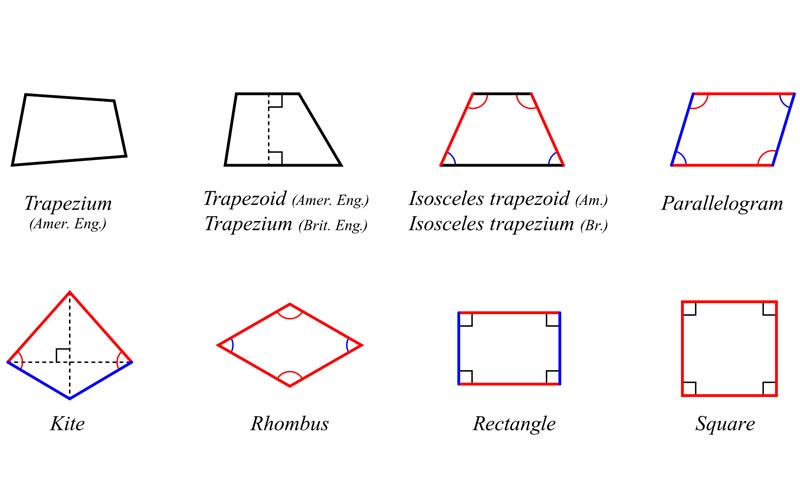
We come across many geometrical figures in our daily lives that do not need mathematical formulas to study. Triangles, circles, squares, rectangles are some of them. A special kind of geometry involves two pairs of equal, opposite and parallel sides constituting the shape called a parallelogram — evident from the name itself. Going by the definition, we can easily discern that a rectangle has the same properties as a parallelogram. What makes them different is the measurement of their sides and the angle between the adjacent sides. It suggests that all rectangles are parallelograms, but not all parallelograms are rectangles. It also gives rise to a set of obvious questions; how many kinds of parallelograms are there? How do we differentiate between different types of parallelograms?
Let’s find out the answers to these questions and understand the various properties that differentiate them in the following pointers.
1. Types of parallelograms
Before we dive into the essentials of a parallelogram, we need to know what is a quadrilateral. Another puzzling name!
Let’s learn the easy definition:
A closed, two-dimensional shape made with four straight lines is called a quadrilateral. It has four vertices or corners.
A parallelogram is an example of a quadrilateral but it is a special one! Both the pairs of opposite sides need to be parallel.
We have to learn about the different kinds of parallelograms in order to differentiate between them later.
In general, there are three different kinds of parallelograms. Rather, special parallelograms. Namely rectangle, square, and rhombus. We can also find examples of other forms of parallelograms. All forms have a few basic properties and also a set of distinguishing properties.
Let us look at the fundamental properties of a parallelogram.
2. Properties of a parallelogram
As discussed earlier, a parallelogram is a special kind of quadrilateral with both pairs of opposite sides parallel to each other. Among the three different types of special parallelograms, four basic properties are common.
- Opposite sides are equal
- Opposite angles are equal
- Diagonals dividing the parallelogram form two congruent (identical) triangles
- Diagonals bisect (cut each other in half) each other
- Consecutive angles are supplementary
- All interior angles will be right-angles if any one of the angles is a right angle
However, the individual properties of different parallelograms are the one which set them apart.
Measurement is the key to draw a perfect parallelogram. For that, take a ruler, draw a straight and horizontal line segment. A few centimetres below, draw another congruent line segment making sure that they are at an equidistance horizontally. Connect the endpoints with a pair of identical and vertical line segments, and you will have a parallelogram. After measuring the interior angles, you will find that the opposite angles are congruent to each other. Following that, connect the opposite corners with a pair of straight lines (diagonals). Following the properties, the diagonals will bisect each other, and each diagonal will form two identical triangles inside the parallelogram.
Now we will understand the distinguishing properties of each kind of parallelogram one by one.
3. Distinguishing properties of different parallelograms
Based on their measurements, we can distinguish between a rectangle, a square, and a rhombus. Before we learn about the differentiating properties of the different parallelograms, we need to take a good look at their definitions individually.
Rectangle
It is a special parallelogram, among others, that has all interior angles of an equal magnitude of 90 degrees. It is an equiangular quadrilateral that inherits all the fundamental properties of a parallelogram. Based on the equivalent magnitude of all the interior angles and supplementing the sum of its opposite angles, it can also be called a cyclic quadrilateral. Apart from the property of having interior angles of equal magnitude, the rectangle possesses other significant properties that differentiate it from other parallelograms.
Properties of a rectangle:
- All the interior angles measure 90 degrees
- Diagonals are congruent
- Both diagonals are of equal length
- Opposite angles of the diagonals bisect each other
- Opposite sides are equal
- The length of the diagonal is also the diameter of the rectangle’s circumcircle
Rhombus
A rhombus is a diamond-shaped geometrical figure with four equal sides. Judging by its figure, a rhombus is also called a diamond or a rhombus diamond. One of its distinguishing features is that its diagonals bisect each other at a right angle. Both diagonals form four congruent right-angled triangles. It is a type of parallelogram since both the pairs of opposite sides are parallel.
Properties of a rhombus:
- Pair of opposite sides are parallel to each other
- Diagonals bisect each at a right angle
- Opposite angles are equal to each other
- Diagonals bisect the angles
- All sides are equal
Square
A square possesses the properties of a rectangle and a rhombus. It is a parallelogram with four identical sides and diagonals that bisect at a right angle. All of its interior angles are equal, i.e., 90 degrees. Since it has similar properties as that of a parallelogram, every square can also be considered a rectangle and a rhombus.
Properties of a square
- The length of both diagonals are equal
- All sides are congruent to each other
- Diagonals bisect each other perpendicularly
- The length of diagonals are greater than the sides
- Both diagonals divide to form two isosceles triangles
4. Similarities between different parallelograms
Although all the parallelograms have distinguishing properties, there are certain similarities among the different kinds that make them part of one family. All the parallelograms must have their base and topsides congruent and parallel to each other. The same goes for its left and right side.
A rectangle has few properties of a square, a rhombus possesses some features of a rectangle and vice versa.
Let us look at the similarities among different kinds of parallelograms.
Square and rectangle
For a rectangle to be a parallelogram, it must have four sides with opposite sides congruent and parallel to each other. Likewise, for a parallelogram to be a rectangle, it must have all four interior angles of equal magnitude, i.e., 90 degrees. Both the congruent diagonals must bisect each other. Similarly, a square also satisfies all the requirements of a rectangle; therefore, a square can also be called a rectangle.
Rhombus and rectangle
Both parallelograms share similar properties to an extent. The opposite sides of both the rhombus and the rectangle are parallel to each other. Both of their adjacent angles are supplementary. Their diagonals bisect each other. Above all, a rhombus can only be called a rectangle when all four of its angles have an equal magnitude of 90 degrees.
5. The distinction between different parallelograms
After discussing the different properties of various kinds of parallelograms, it is evident that apart from the basics, there are certain exceptions that make them special on their own. Despite their similarities and dissimilarities, all the parallelograms’ geometry’s distinctiveness draws our interest to study them.
Let us explore the dissimilarities among the different kinds of parallelograms.
Square and rhombus
A parallelogram is called a square only when it has four congruent right angles and four congruent sides. Both kinds of parallelograms have four congruent sides. Whereas, a rhombus does not always require congruent interior angles, i.e., 90 degrees. The lengths of both the diagonals of a rhombus are of different measures. In contrast, both the diagonals of a square are of equal measure.
Square and rectangle
A square has four congruent sides, but a rectangle has only opposite sides of equal length. Additionally, the diagonals of a square bisect each other perpendicularly. Whereas, the diagonals of a rectangle are not perpendicular bisectors of each other. A square is a special kind of rectangle with all sides identical to each other.
In conclusion, along with the rectangle, other geometric figures also constitute a family of different parallelograms. Each of them is unique. There is a fair number of similarities and dissimilarities among different parallelograms. To figure that out, we have to understand various aspects of measurement. The sides’ length, and the angular value of the vertices, among others, define the properties of each kind of parallelogram. For your precision, the measurement made easy with Cuemath will help you distinguish among different parallelograms.